Dans la biographie qu'il a consacrée à Alan Turing¹, Andrew Hodges mentionne un épisode assez savoureux de la vie académique du père de l'informatique : sa brève participation aux cours que donnait Ludwig Wittgenstein à Cambridge en 1939 sur les « fondements des mathématiques ». L'objectif de Wittgenstein en ce qui concerne ces dernières est assez connu : il s'agissait de les déloger de leur piédestal multiséculaire, d'en faire un phénomène anthropologique parmi d'autres, autrement dit de les considérer comme un pan de l'histoire naturelle de l'humanité, avec ses coutumes et ses règles unanimement acceptées et tacitement reconduites. Pour W., l'idée qu'il puisse y avoir un paradoxe dans un énoncé (mathématique ou autre) ne semblait pas poser de problème majeur. Exemple de discussion avec Turing : « [...] si un homme dit "je mens", nous disons qu'il s'ensuit qu'il ne ment pas, d'où il s'ensuit qu'il ment et ainsi de suite. Bien, et alors ? Vous pouvez poursuivre jusqu'à la congestion. Pourquoi pas ? Peu importe... »². Turing, par contre, n'était pas de cet avis. Il était ce qu'on pourrait appeler un « puriste » des mathématiques, qui voyait dans ces dernières un système complet qui se devait d'être stable et consistant. En guise d'argumentation, il donnait à W. des réponses d'ingénieur : « Le mal n'adviendra pas à moins qu'il y ait une application, dans laquelle un pont pourrait tomber ou quelque chose de ce type ». Ce à quoi W. répondait entre autres par : « [...] Si quelque chose tourne mal — si le pont s'écroule —, alors votre erreur était du type de celles consistant à utiliser une mauvaise loi naturelle ». Mais Turing n'en démordait pas : « Vous ne pouvez pas avoir confiance dans l'application de vos calculs jusqu'à ce que vous sachiez qu'ils ne contiennent pas une contradiction cachée », ou encore : « Bien que vous ne sachiez pas que le pont tombera s'il n'y a pas de contradiction, il est presque certain que s'il y a des contradictions, quelque chose tournera mal ». Et la conversation tombait dans l'impasse, car à ce genre de propos, W. répondait que, jusqu'à présent, rien n'avait jamais tourné mal de cette façon. — Environ un an plus tard, le pont de Tacoma s'effondrait en raison d'une erreur de conception, ce qui rend a posteriori la discussion entre W. et T. très amusante³. (Cela dit, le fait que le pont de Tacoma s'est écroulé en novembre 1940 ne constitue nullement un « contre-exemple » de ce que disait Wittgenstein en 1939 à propos des mathématiques.)

En lisant la prose de Roger Penrose dans son ouvrage concernant les lois de l'univers⁴, je retombe sur l'un de ces discours sur les mathématiques que Wittgenstein essayait à tout prix de saper. Penrose est, dans un certain sens, encore « pire » que Turing : c'est un platonicien qui aborde le monde mathématique avec une sorte de dévotion béate. Il se comporte par moment comme un prêtre chargé de nous communiquer une bonne nouvelle : que les mathématiques sont intrinsèquement belles, vraies, magiques... Chez Penrose, la magie n'est en effet jamais bien loin. Le mot revient très souvent dans ses explications et est même utilisé dans le titre du chapitre 4 : « La magie des nombres complexes ». Plus fort encore : dans le chapitre 5 consacré à la géométrie des logarithmes, Penrose aborde la fameuse identité d'Euler qui met en relation, avec une impressionnante économie de moyens, cinq nombres parmi les plus importants des mathématiques :

e^πi + 1 = 0

Et il dit de cette formule qu'elle « réunit les cinq nombres fondamentaux 0, 1, i, π et e dans une expression quasiment mystique »⁵ (c'est moi qui mets en italique). Mais pourquoi donc utiliser le terme « mystique », qui fait référence aux mystères, aux vérités cachées et, en définitive, à la religion ? L'identité d'Euler est-elle de l'ordre de la révélation ? (Non, l'identité d'Euler est simplement... l'identité d'Euler.) Pour mieux comprendre la vision de Penrose quant aux mathématiques, il faut remonter au chapitre 1, où il met clairement en avant ce qu'il appelle ses « préjugés » en la matière. Penrose ne voit pas seulement les mathématiques comme un ensemble de connaissances permettant de modéliser avec une précision d'horloger le monde qui nous entoure ; il les voit aussi dotées d'une « existence » propre. Ainsi imagine-t-il un « monde mathématique platonicien » qui a le redoutable avantage, pour un scientifique, de constituer une « norme extérieure objective qui ne dépend pas de nos opinions individuelles ou de notre culture »⁶. P. ajoute par ailleurs que cette « existence » platonicienne pourrait « aussi concerner d'autres domaines que les mathématiques, comme la morale ou l'esthétique ». Ainsi se dit-il « tout à fait prêt à admettre l'existence » d'idéaux absolus comme le beau ou le bien.

Ce n'est pas la première fois que j'observe un scientifique parler d'éthique ou d'esthétique et, à chaque fois, je suis marqué par le discours qu'il tient : un discours ingénu, presque enfantin. Une des idées de Penrose est qu'il existe un lien direct entre la beauté (ou la simplicité) d'un concept mathématique et sa vérité... au point qu'il continue sur sa lancée : si, en mathématiques, la vérité découle souvent de la beauté, pourquoi ne serait-ce pas le cas pour d'autres pans de la connaissance, comme par exemple la question de pouvoir décider de ce qui est bien et de ce qui est mal ? — La vision de P. à ce sujet me fait penser à celle de Noam Chomsky aux prises avec Michel Foucault dans le célèbre débat sur la nature humaine (1971). Chomsky se comporte en rationaliste et en logicien, dans la lignée de Bertrand Russell. Il est d'une régularité exemplaire sur le terrain de la morale : il a développé l'idée qu'il existait des absolus, des fondamentaux propres à toute l'humanité (l'amour, la justice, la bonté, etc.), dépassant le cadre d'une société donnée. Devant lui, Foucault est beaucoup plus prudent, circonspect, précis. Il ramène ces concepts sur le terrain historique. Il les relativise. La justice, par exemple, n'est pas une entité éthérée, pure, suspendue au-dessus des hommes et du temps ; le concept de « justice » se développe à l'intérieur du cadre philosophique, social, politique d'une civilisation, à l'intérieur d'un système de règles. Le désaccord (énorme) entre Chomsky et Foucault à ce sujet est très bien exprimé dans leur dernière intervention, quelques minutes avant les questions du public :

Chomsky (en anglais) : « Je pense qu'il est trop hâtif de caractériser nos actuels systèmes de justice comme de simples systèmes d'oppression de classe. [En plus de représenter de tels systèmes], ils représentent aussi une sorte de tâtonnement à travers les vrais concepts humains de justice, de décence, d'amour, de gentillesse, de sympathie, qui je pense sont réels. »⁷
Foucault : « [...] contrairement à ce que vous pensez, je ne peux pas m'empêcher de croire que cette notion de nature humaine, cette notion de bonté, de justice, d'essence humaine, de réalisation de l'essence humaine ; tout ça, ce sont des notions et des concepts qui ont été formés à l'intérieur de notre civilisation, dans notre type de savoir, dans notre forme de philosophie, et que par conséquent, ça fait partie même de notre système de classes et qu'on ne peut pas, aussi regrettable que ce soit, [...] faire valoir ces notions pour décrire ou justifier un combat qui devrait, qui doit en principe bouleverser les fondements mêmes de notre société. Il y a là une extrapolation dont je n'arrive à trouver la justification historique. »⁸

Il y a un lien évident entre la vision de Chomsky dans cette discussion philosophique et ce que dit Penrose des mathématiques dans son ouvrage. Il est question dans les deux cas d'un monde indépendant de l'existence humaine, un monde parfait, idéal, à l'intérieur duquel l'humanité peut en quelque sorte piocher. Mais si ce genre de discours paraît particulièrement suspect quand il s'intéresse à l'éthique ou à l'esthétique, il semble presque naturel quand il touche aux mathématiques : au-delà des signes et des notations (forcément propres à un convention d'écriture donnée), si deux civilisations humaines complètement indépendantes l'une de l'autre s'intéressaient, par exemple, aux propriétés fondamentales de certaines formes géométriques, pourraient-elles diverger ? La question du vrai et du faux d'un énoncé semble beaucoup plus tranchée en mathématiques que dans toute philosophie. On peut sans problème concevoir (même si cela peut nous sembler abject) une société dans laquelle tuer des individus est considéré comme éthique ; par contre, peut-on imaginer une société dans laquelle la somme des angles d'un triangle sur le plan euclidien est différente d'un angle plat ? — Mais s'il ne s'agissait plus de comparer les connaissances mathématiques de deux civilisations humaines indépendantes, mais plutôt de, disons, d'un côté l'humanité et de l'autre une conscience extérieure à l'humanité (une hypothétique civilisation extraterrestre ?), y aurait-il encore consensus sur la somme des angles d'un triangle ? Peut-on seulement répondre à cette question ? En tout cas, Penrose répondrait sans aucun doute par l'affirmative. Pour lui, les mathématiques sont strictement universelles et les mathématiciens, de simples explorateurs : ils n'inventent rien, ils ne font que découvrir un territoire qui existe de tout temps et en tout lieu. Prenant l'exemple de l'ensemble de Mandelbrot, Penrose déclare :

« Ce que je voudrais souligner ici, c'est que personne — pas même Benoît Mandelbrot lui-même lorsqu'il a découvert pour la première fois la complexité incroyable des petits détails de cet ensemble — n'aurait pu deviner son extraordinaire richesse. L'ensemble de Mandelbrot n'est en aucun cas le fruit d'un esprit humain. Cet ensemble réside simplement, objectivement, dans les mathématiques elles-mêmes. [...] Son existence n'est à trouver que dans le monde platonicien des formes mathématiques. »

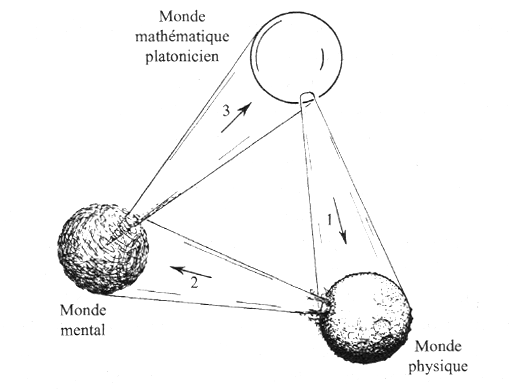
Toujours dans le premier chapitre de son livre, Penrose propose un schéma de ce « monde platonicien des formes mathématiques » mis en relation avec deux autres mondes autonomes, le « monde physique » et le « monde mental ». Dans la vision de Penrose, le monde mathématique — ou plus exactement une portion de celui-ci — forge l'ensemble du monde physique (autrement dit, derrière tout phénomène physique, il y a un arrière-plan mathématique) ; une portion du monde physique forge l'ensemble du monde mental (autrement dit, tout état mental est un phénomène qui appartient au monde physique) ; enfin, une portion du monde mental est capable d'atteindre l'ensemble du monde mathématique (autrement dit, les mathématiques, à la base du monde physique, sont entièrement accessibles à la raison humaine). Penrose est très optimiste.

Deux pages plus loin, il propose un autre schéma qui, écrit-il, permet de transgresser ses préjugés (voir ici) : dans ce schéma, les trois mondes sont toujours présents, mais les cônes qui les relient sont plus ténus, de telle manière que le monde mathématique ne forge plus qu'une partie du monde physique (autrement dit, une partie du monde physique échappe à toute formalisation mathématique), etc. — J'ai beau tourner ce second schéma dans tous les sens, je ne vois pas en quoi il transgresse vraiment les préjugés de l'auteur : les trois mondes sont toujours représentés et les liens entre eux aussi. Tout au plus ces liens ne sont-ils pas aussi forts. Imaginer l'existence de trois mondes en interaction constante, c'est déjà un préjugé.

J'adore toujours autant ce livre — grâce à lui, j'apprends beaucoup de nouvelles notions en très peu de temps —, mais je me serais bien passé de cette vision des mathématiques comme entités presque magiques. À mon sens, dire que l'identité d'Euler est belle, miraculeuse, voire « quasiment mystique », équivaut presque à observer un flocon de neige au microscope électronique et à s'exclamer que, décidément, la nature est formidablement bien foutue. Pourquoi s'émerveiller ? Les mathématiques sont ce qu'elles sont parce que le monde est ce qu'il est. Comment pourrait-il en être autrement ? Ce que je veux exprimer ici est quelque chose qui n'est que très difficilement exprimable. Une tentative serait de dire : « Nous sommes à l'intérieur d'un système. Comment pourrions-nous être à la fois à l'intérieur de quelque chose et en apercevoir l'extérieur ? » Ou encore : « Les mathématiques constituent tout ce qui est pensable en mathématiques. Et tout ce qui n'est pas pensable ne peut pas être pensé. » Dire cela, c'est ne pas dire grand-chose ; c'est tourner en rond, à l'instar d'un hamster dans sa roulette. Cependant je ne suis pas certain que nous puissions faire autre chose que de tourner en rond. — Nous sommes tous des hamsters... mais légèrement plus intelligents.

________________________________________
¹ Andrew Hodges, Alan Turing ou l'énigme de l'intelligence, Paris, Éditions Payot, 1988. [Alan Turing: The Enigma of Intelligence, 1983.] Le titre anglais constitue un petit clin d'œil à la machine de cryptage allemande Enigma, dont le déchiffrement doit beaucoup à Turing (et aussi à trois mathématiciens polonais précurseurs, moins connus mais cependant tout aussi ingénieux : Marian Rejewski, Jerzy Rozycki et Henryk Zygalski).
² Ibidem, p. 138. Les citations de Turing et Wittgenstein qui suivent proviennent du même endroit. Par moment, je me suis permis de modifier la traduction pour rester plus fidèle au texte original. On trouvera une retranscription plus complète de cette discussion (en anglais) sur cette page.
³ La seule victime de l'effondrement fut... un cocker anglais à trois jambes — cette dernière information a été donnée par la maîtresse du chien en 1975 — du nom de Tubby, abandonné sur le siège arrière d'une voiture par son propriétaire, le reporter Leonard Coatsworth, alors que le pont se détériorait rapidement. Il ne faut pas trop en vouloir au maître du chien : il a apparemment essayé de le sauver, de même que deux autres personnes (dont un ingénieur dépêché sur place pour observer le tangage du pont : cet homme a même essayé d'extraire l'animal paniqué de la voiture, mais a dû renoncer pour éviter les morsures). Quelques minutes plus tard, la voiture et le chien plongeaient dans les eaux du détroit de Tacoma. Mais ceci est une autre histoire, comme dirait l'autre... Une histoire qui n'a rien à avoir avec le sujet principal de ce texte. Pour en savoir plus sur ce chien, voici un article assez précis en anglais. On trouvera aussi plein d'informations sur Tubby le cocker anglais sur cette page dédiée à l'histoire du pont de Tacoma.
⁴ Roger Penrose, À la découverte des lois de l'univers. La prodigieuse histoire des mathématiques et de la physique, Paris, Odile Jacob, 2007. (Voir l'article précédent pour les détails.)
⁵ Ibidem, p. 87.
⁶ Toutes les citations de Penrose qui suivent proviennent du chapitre 1 de son livre, intitulé « Aux sources de la science », p. 7-22.
⁷ « I think it's too hasty to characterise our existing systems of justice as merely systems of class oppression. I don't think that they are that. I think that they embody systems of class oppression and they embody elements of other kinds of oppression, but they also embody a kind of groping towards the true humanly, valuable concepts of justice and decency and love and kindness and sympathy, and so one, which I think are real. » (Lien vers cet extrait.)
⁸ Lien vers cet extrait.